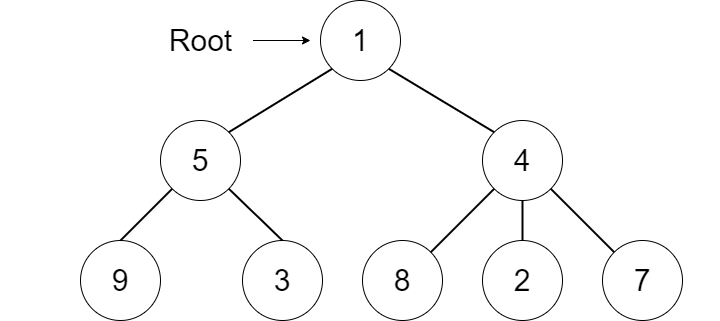
Trees are an important type of data structure that can optimize the amount of time spent searching for a piece of data. A tree can be visualized as a hierarchy of nodes where the top node is the root of the tree. The root node can branch off to multiple nodes which all represent child nodes. The child nodes can also further branch off having their own children nodes. A node that does not contain any child nodes is referred to as a “leaf” node. A node above a child node is often referred to as the parent for that subsection of the tree.
In many programming exercises, the trees are defined as binary trees which sets the constraint that all of the nodes in the tree can only have either 0, 1, or 2 child nodes (hence the term binary).
Furthermore, a binary tree can be even more specialized if it is a binary search tree. A binary search tree must not only adhere to the constraints of a binary tree, but it must also fit the condition that all the nodes on the left side must have a smaller value than the parent node and all the nodes on the right side must have a larger value than the parent node. This constraint must be followed by all the nodes in the tree.
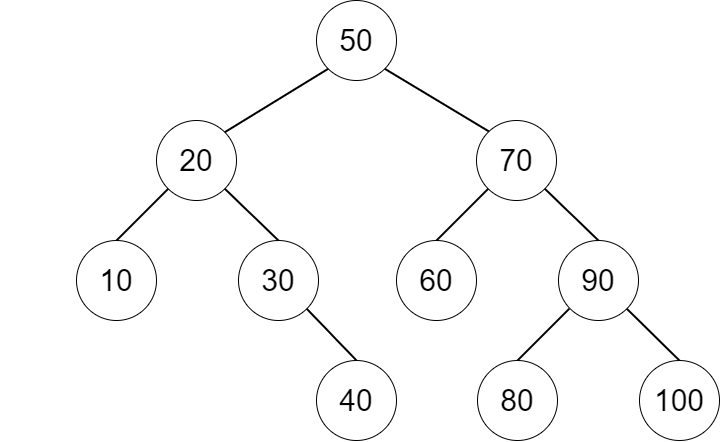
Along with understanding how the tree data structure works comes with knowing how to access the data contained in each node. There are many different techniques that can be implemented to visit all of the nodes in a tree, however the three most common methods are in-order traversal, pre-order traversal, and post-order traversal. The output of each of these traversal techniques are demonstrated on the example tree below. Note that the example tree is a binary search tree, however it is not essential for it to be one in order to run the traversals.
The algorithms for all three of the traversals can be found in the code implementation section below.
One of the most common types of tree data structures are binary search trees and we will be implementing this type of tree in the code below. As we can recall, a binary search tree is a tree where each node has up to two child nodes and that the values of the left child nodes are less than the parent node while the values of the right child nodes are greater than the parent node.
The structure of a tree is very similar to other data structures such as a LinkedList since they both contain nodes that link to other nodes. Trees however may not be linear since the parent node has access to a left node and right node. We will create the "TreeNode" class which resembles a simple node class, however it will contain instances for the left and right node variables.
class
TreeNode{
TreeNode left;
TreeNode right;
int
data;
public
TreeNode(
int
data){
this
.data = data;
}
}
To finish off the basic structure of the binary search tree, we will add a method which will allow us to add data to the tree. This method is pretty straight forward as it will check to see if the new value we want to add is less than or greater than the root node's value. If the value is less than the root node we will check to see if the left child node is occupied and if it is then a recursive call to the function will be made using the left node. If the left node is not occupied then the value will be placed in that node location. The same logic is applied to the right side of the tree if the new value is greater than the root node's value.
class
TreeNode{
TreeNode left;
TreeNode right;
int
data;
public
TreeNode(
int
data){
this
.data = data;
}
public void
add(
int
data){
if
(data <
this
.data){
if
(left ==
null
){
left =
new
TreeNode(data);
}
else
{
left.add(data);
}
}
if
(data >
this
.data){
if
(right ==
null
){
right =
new
TreeNode(data);
}
else
{
right.add(data);
}
}
}
}
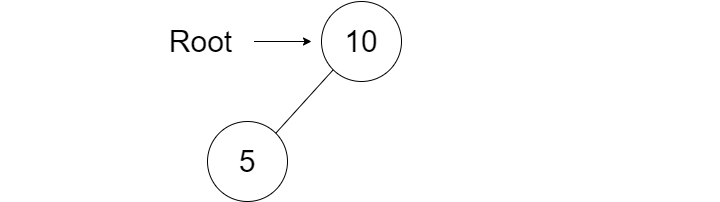
With the binary search tree class in place, we can walk through an example in our main function. The first step in creating our tree is to create an instance of the TreeNode class. This will be the root of our tree and all other values will be an extension from this node.
public static void
main(String[] args){
TreeNode root =
new
TreeNode(10);
}
We will now add a left child node to the graph by calling the add() method that we previously implemented and passing in a parameter containing the integer 5. We know that this will be a left node because 5 is less than the root node value of 10.
public static void
main(String[] args){
TreeNode root =
new
TreeNode(10);
root.add(5);
}
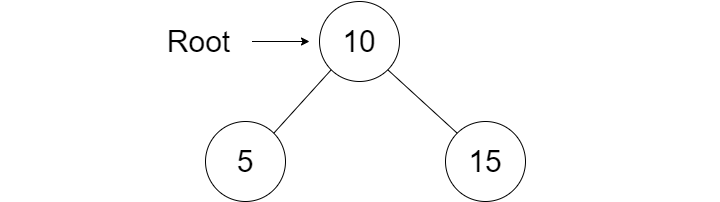
Similarly we can now add a right node by calling the add() method with a parameter value greater than 10. We will call the add() method passing a value of 15.
public static void
main(String[] args){
TreeNode root =
new
TreeNode(10);
root.add(5);
root.add(15);
}
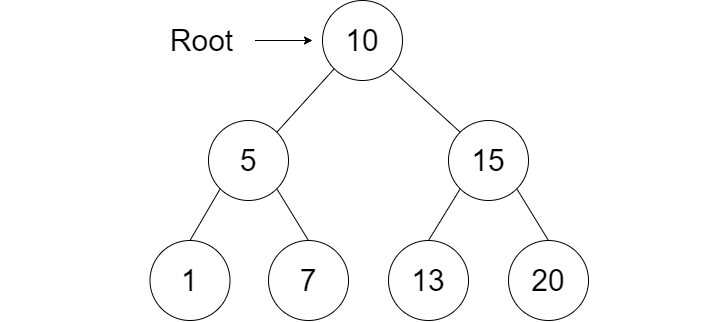
We can continue to add nodes to our tree by calling the add() method. Let's add the values 1, 7, 13, and 20 in that respective order.
public static void
main(String[] args){
TreeNode root =
new
TreeNode(10);
root.add(5);
root.add(15);
root.add(1);
root.add(7);
root.add(13);
root.add(20);
}
Three common traversal methods that we will implement are the in-order traversal, pre-order traversal, and post-order traversal. The code for traversing a tree is very simple and the only difference between the three traversal methods are the order in which the code is written.
The in-order traversal will print the left node, parent node, then right node value in that order. If the left or right nodes have child nodes then a recursive call must be made.
public static void
inOrderTraversal(TreeNode parent){
if
(parent.left !=
null
){
inOrderTraversal(parent.left);
}
System.out.print(parent.data + " ");
if
(parent.right !=
null
){
inOrderTraversal(parent.right);
}
}
Output:
1 5 7 10 13 15 20
The pre-order traversal will print the parent node, left node, then right node value in that order. If the left or right nodes have child nodes then a recursive call must be made.
public static void
preOrderTraversal(TreeNode parent){
System.out.print(parent.data + " ");
if
(parent.left !=
null
){
preOrderTraversal(parent.left);
}
if
(parent.right !=
null
){
preOrderTraversal(parent.right);
}
}
Output:
10 5 1 7 15 13 20
The post-order traversal will print the left node, right node, then parent node value in that order. If the left or right nodes have child nodes then a recursive call must be made.
public static void
postOrderTraversal(TreeNode parent){
if
(parent.left !=
null
){
postOrderTraversal(parent.left);
}
if
(parent.right !=
null
){
postOrderTraversal(parent.right);
}
System.out.print(parent.data + " ");
}
Output:
1 7 5 13 20 15 10