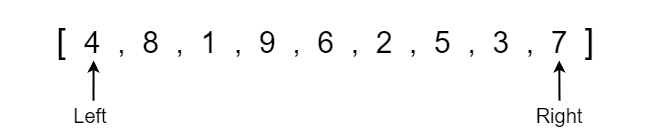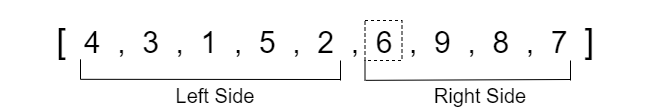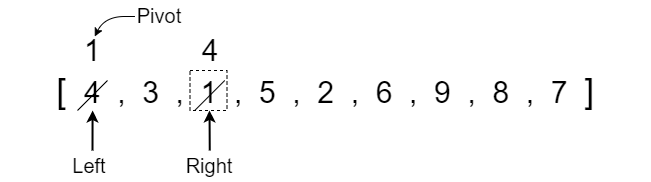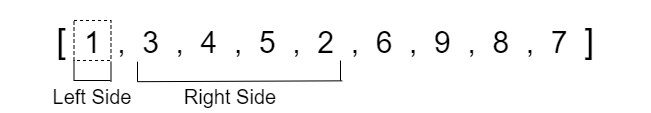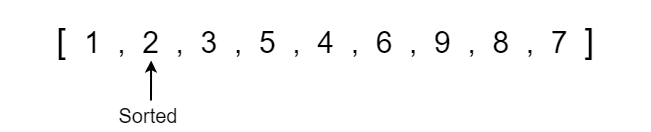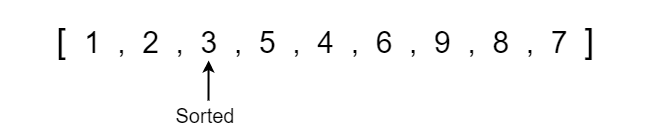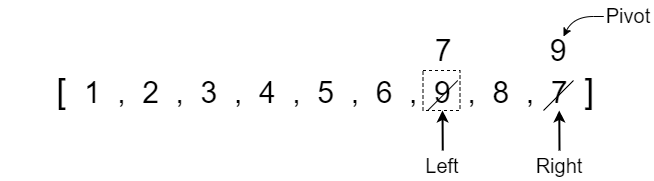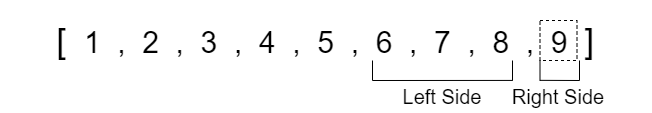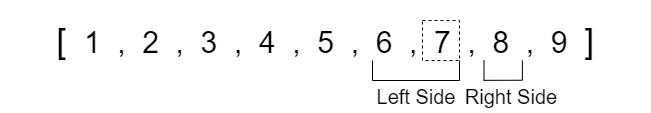Quick sort is an advanced sorting algorithm that functions by swapping values around a pivot element. Values greater than or equal to the pivot will be shifted to the right side of the array while values less than the pivot will be shifted to the left side. This creates a partition in the array where we can then call quick sort recursively on each side until all of the elements land in their sorted positions.
The best way to quickly grasp the concept of quick sort is to visually see an example of each step that is occurring in the algorithm. We will walk through an example of this algorithm using the following unsorted integer array.
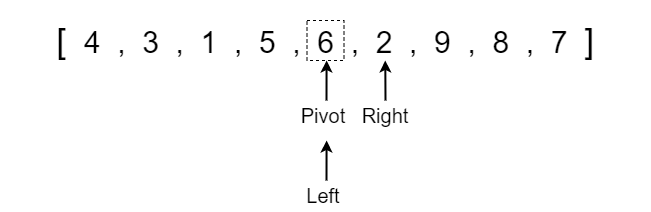
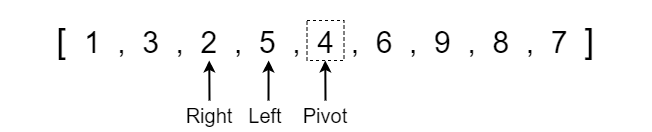
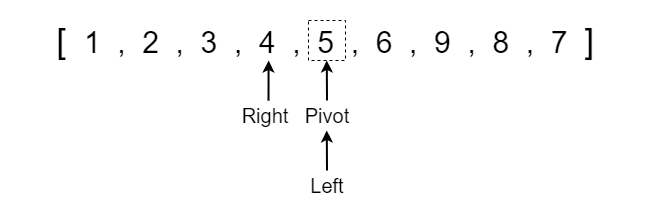
Before we start applying the quick sort algorithm we need to discuss the initialization of a few variables. Firstly, we need to create two variables placed at opposite ends of the section of the array that we are sorting. This will be a left pointer variable at index 0 and the right pointer variable at the last index of the array. Keep in mind that as we call quick sort recursively, the left and right pointers will be at the opposite ends of the particular SECTION of the array that we are sorting.
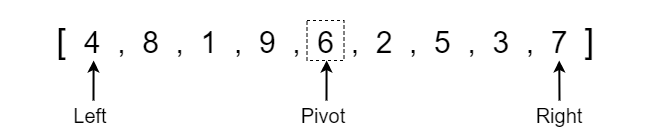
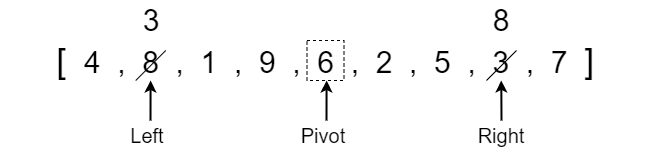
Once we have our left and right pointers defined, we need to determine what the pivot element should be. For simplicity, we will set the pivot value equal to the middle element between the left and right indexes. In our example, the middle index is 4 which contains a value of 6.
Note that the pivot is equal to the VALUE at the middle index whereas the left and right pointers refer to the index position. The dotted box represents that the pivot is equal to the value rather than the index position.
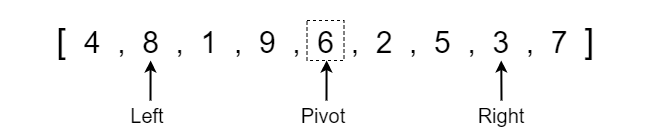
We can now perform the main steps of the quick sort algorithm which is to move all values less than the pivot value to the left side and all the values greater than the pivot to the right side. To do this, we first check what the value at the left pointer is. We want to find a value that is greater than or equal to the pivot for the left pointer to swap with the right pointer. The left pointer is pointing to a value of 4 which is less than the pivot value so we will move the left pointer up one index.
The left pointer is now pointing at a value of 8 which is greater than or equal to the pivot element so we can stop moving the left pointer.
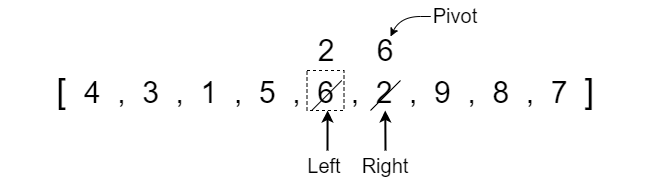
We now want to check the value at the right pointer. Similar to the left pointer, we want to find a value that is less than or equal to the pivot. Since the right pointer is pointing at a value of 7 which is greater than the pivot element, we have to move it one index position to the left. To do this, we decrease the right pointer index value by 1.
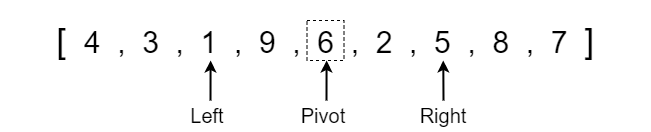
The right pointer is now pointing at the value 3 which is less than the pivot so we stop moving it at this index position. We now need to compare whether the left pointer index has exceeded the right pointer index and if not then we swap the values. The left pointer is at index position 1 while the right pointer is at index position 7, therefore left is not greater than right so we swap the values.
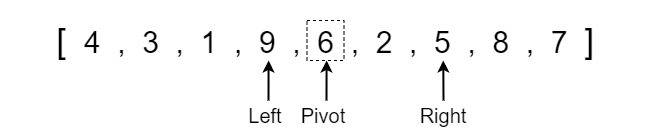
After swapping the values at the left and right indexes, we move the left pointer up one index and move the right pointer down one index.
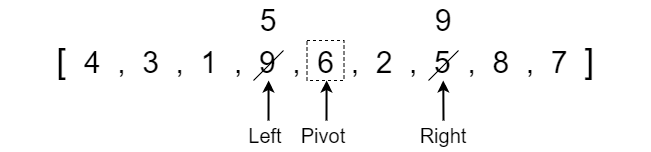
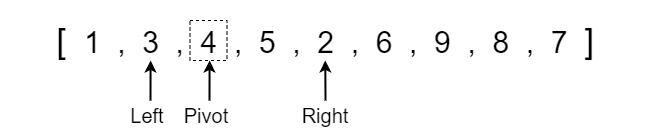
We now compare whether the left index pointer has exceeded the right index pointer and if not then we continue to search for values that need to be swapped. Left is not greater than right so we check if the value at the left pointer is greater than or equal to the pivot. It is not greater than or equal so we move the left pointer up one index.
The left pointer has a value of 9 which is greater than the pivot so we stop moving it. We take a look at the right pointer and we see that it has a value of 5 which is less than the pivot so we stop. We again compare if the left pointer index has exceeded the right pointer index which it has not so we swap the values.
Again after swapping the values, we move the left pointer up and the right pointer down.
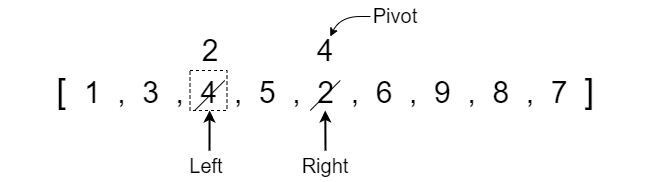
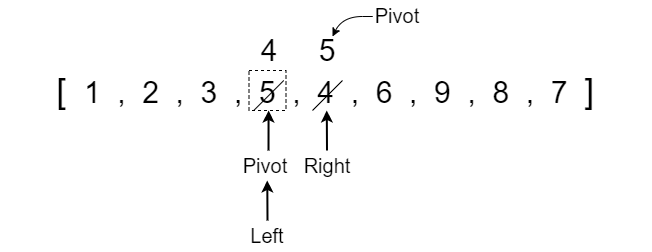
The left pointer now has a value of 6 which is equal to the pivot value so we stop moving it and the right pointer has a value less than the pivot so it also does not move. We can swap the values because the left pointer index is still less than the right pointer index.
Notice that the pivot will always follow the value that it was pointing at because it is equal to the value and is NOT a reference to an index position. Once we swap the values we need to increase the left pointer and decrease the right pointer.
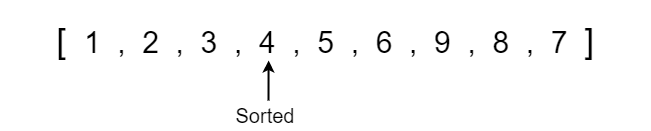
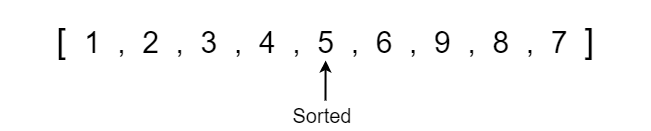
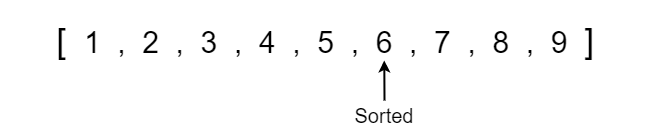
Now we can see that the left pointer has exceeded the right pointer so we are done swapping values around the pivot. If we take a moment to analyze the array, we can see that all the values less than the pivot value 6 are on the left side and all values greater than or equal to the pivot are on the right side. This partition happens at the left index which is important to note because we will need this partition value when we run quick sort recursively in the actual code.
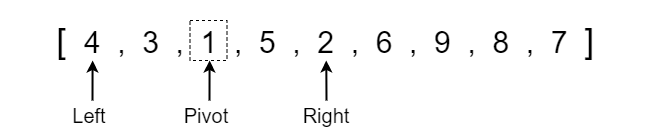
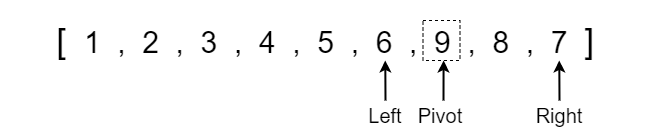
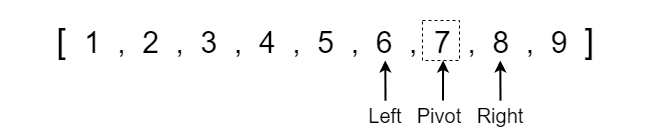
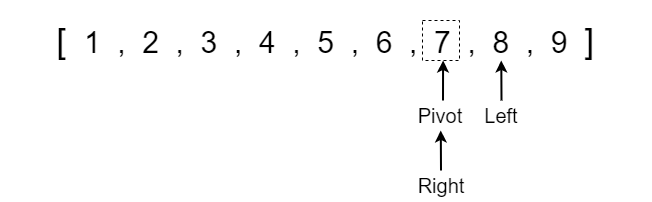
We now see that the array is becoming progressively more sorted, so all we have to do is continue to run quick sort on each respective partition until the array becomes completely sorted. When running quick sort recursively, we will run into a point where the left or right side may only contain one element which is the base condition where we no longer have to run quick sort since a single element is already sorted in position.
I will quickly show each step of the recursive quick sort function calls until the array becomes completely sorted.
Quick sort is a simple algorithm to implement once we understand exactly what is happening at each individual step. We will break up the quick sort algorithm into a couple different functions to keep our code clean and divide up the tasks. Firstly, we need to create the quickSort() function that takes in an integer array to be sorted.
public static void
quickSort(
int
[] nums){
}
Inside of this function we simply make a call to our recursive quick sort function to kick off the recursive process of this algorithm. The recursive function will be called quickSortRecursive() and will take in three parameters. The first parameter being the integer array to be sorted, the second being the left index position, and the third being the right index position. We want to set the left index to the start of the unsorted array which will be at index 0 and the right index to the last index position of the array.
public static void
quickSort(
int
[] nums){
quickSortRecursive(nums, 0, nums.length-1);
}
We can now implement the quickSortRecursive() function. As described above, this function takes in three parameters. Note that we call the left index position 'leftStart' and the right index position 'rightEnd' which denotes the section that quick sort is being applied.
public static void
quickSort(
int
[] nums){
quickSortRecursive(nums, 0, nums.length-1);
}
public static void
quickSortRecursive(
int
[] nums,
int
leftStart,
int
rightEnd){
}
Inside of this function we need to first add the base case condition. This is the condition that should cause the recursive calls to terminate. This will happen when the leftStart pointer is equal to or greater than the rightEnd pointer. If the leftStart pointer is equal to the rightEnd pointer then we immediately know that there is only one element to be sorted. This means that it is already in the correctly sorted position so there is nothing left we need to do.
public static void
quickSort(
int
[] nums){
quickSortRecursive(nums, 0, nums.length-1);
}
public static void
quickSortRecursive(
int
[] nums,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
}
The next step is to get the pivot value. As we already know, the trick to this algorithm revolves around swapping values around the pivot element. REMEMBER that the pivot refers to the value and not an index position. To get the pivot value, we will need to find the middle index position using leftStart and rightEnd then assign pivot with the value at the middle index position of the nums array.
public static void
quickSort(
int
[] nums){
quickSortRecursive(nums, 0, nums.length-1);
}
public static void
quickSortRecursive(
int
[] nums,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
pivot = nums[leftStart + (rightEnd - leftStart)/2];
}
Once we have our pivot element we can start swapping values around it to partition the values. Remember we want to keep track of the partition index since we will be running quick sort recursively on the left side of the partition as well as the right side of the partition. We will write the logic for swapping the values and retrieving the partition index in a separate function called partition().
public static void
quickSort(
int
[] nums){
quickSortRecursive(nums, 0, nums.length-1);
}
public static void
quickSortRecursive(
int
[] nums,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
pivot = nums[leftStart + (rightEnd - leftStart)/2];
int
index = partition(nums, leftStart, rightEnd, pivot);
}
Lastly, after swapping the values and getting the partition index we call quick sort recursively on the left and right sides.
public static void
quickSort(
int
[] nums){
quickSortRecursive(nums, 0, nums.length-1);
}
public static void
quickSortRecursive(
int
[] nums,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
pivot = nums[leftStart + (rightEnd - leftStart)/2];
int
index = partition(nums, leftStart, rightEnd, pivot);
quickSortRecursive(nums, leftStart, index-1);
quickSortRecursive(nums, index, rightEnd);
}
Now that we have completed the quickSortRecursive() function, the last thing we need to implement is the partition function that performs the swapping of values and return the partition index. In this partition() function we will have 4 parameters, the array to be sorted, the left index position, the right index position, and the pivot value.
public static void
quickSort(
int
[] nums){
quickSortRecursive(nums, 0, nums.length-1);
}
public static void
quickSortRecursive(
int
[] nums,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
pivot = nums[leftStart + (rightEnd - leftStart)/2];
int
index = partition(nums, leftStart, rightEnd, pivot);
quickSortRecursive(nums, leftStart, index-1);
quickSortRecursive(nums, index, rightEnd);
}
public static int
partition(
int
[] nums,
int
left,
int
right,
int
pivot){
}
The partition function is where all the magic happens. We want to continue to swap values between the left and right indexes as long as the left index is less than or equal to the right index.
public static void
quickSort(
int
[] nums){
quickSortRecursive(nums, 0, nums.length-1);
}
public static void
quickSortRecursive(
int
[] nums,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
pivot = nums[leftStart + (rightEnd - leftStart)/2];
int
index = partition(nums, leftStart, rightEnd, pivot);
quickSortRecursive(nums, leftStart, index-1);
quickSortRecursive(nums, index, rightEnd);
}
public static int
partition(
int
[] nums,
int
left,
int
right,
int
pivot){
while
(leftStart <= rightEnd){
}
}
Inside of the while loop we need to check if the left index has a value greater than or equal to the pivot. If not we continue to move the left pointer to the right.
public static void
quickSort(
int
[] nums){
quickSortRecursive(nums, 0, nums.length-1);
}
public static void
quickSortRecursive(
int
[] nums,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
pivot = nums[leftStart + (rightEnd - leftStart)/2];
int
index = partition(nums, leftStart, rightEnd, pivot);
quickSortRecursive(nums, leftStart, index-1);
quickSortRecursive(nums, index, rightEnd);
}
public static int
partition(
int
[] nums,
int
left,
int
right,
int
pivot){
while
(leftStart <= rightEnd){
while
(nums[left] < pivot){
left++;
}
}
}
Similarly, we want to check if the right index value is less than or equal to the pivot value. If not, we will move the right pointer towards the left.
public static void
quickSort(
int
[] nums){
quickSortRecursive(nums, 0, nums.length-1);
}
public static void
quickSortRecursive(
int
[] nums,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
pivot = nums[leftStart + (rightEnd - leftStart)/2];
int
index = partition(nums, leftStart, rightEnd, pivot);
quickSortRecursive(nums, leftStart, index-1);
quickSortRecursive(nums, index, rightEnd);
}
public static int
partition(
int
[] nums,
int
left,
int
right,
int
pivot){
while
(leftStart <= rightEnd){
while
(nums[left] < pivot){
left++;
}
while
(nums[right] > pivot){
right--;
}
}
}
Once we have found a left value and a right value that we want to swap we need to check whether the left pointer has exceeded the right pointer before swapping. If the left pointer has not exceeded the right pointer then we can swap the values and move the left pointer up one position and the right pointer down a position.
public static void
quickSort(
int
[] nums){
quickSortRecursive(nums, 0, nums.length-1);
}
public static void
quickSortRecursive(
int
[] nums,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
pivot = nums[leftStart + (rightEnd - leftStart)/2];
int
index = partition(nums, leftStart, rightEnd, pivot);
quickSortRecursive(nums, leftStart, index-1);
quickSortRecursive(nums, index, rightEnd);
}
public static int
partition(
int
[] nums,
int
left,
int
right,
int
pivot){
while
(left <= right){
while
(nums[left] < pivot){
left++;
}
while
(nums[right] > pivot){
right--;
}
if
(left <= right){
int
temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
left++;
right--;
}
}
}
Lastly, once we have completed swapping all the values to their correct sides we must return the partition point. Recall that this partition point is equal to the value of the left index pointer. Therefore the completed quick sort algorithm is as follows.
public static void
quickSort(
int
[] nums){
quickSortRecursive(nums, 0, nums.length-1);
}
public static void
quickSortRecursive(
int
[] nums,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
pivot = nums[leftStart + (rightEnd - leftStart)/2];
int
index = partition(nums, leftStart, rightEnd, pivot);
quickSortRecursive(nums, leftStart, index-1);
quickSortRecursive(nums, index, rightEnd);
}
public static int
partition(
int
[] nums,
int
left,
int
right,
int
pivot){
while
(left <= right){
while
(nums[left] < pivot){
left++;
}
while
(nums[right] > pivot){
right--;
}
if
(left <= right){
int
temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
left++;
right--;
}
}
return
left;
}