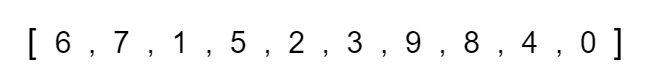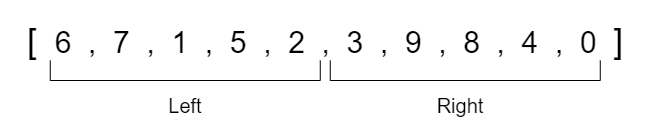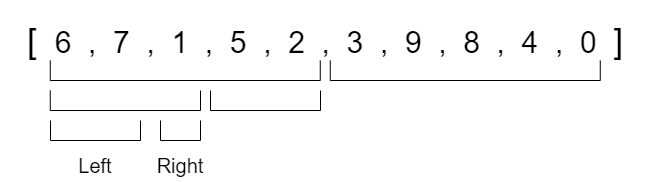Merge sort is an advanced sorting algorithm that is very commonly used due to its quick and consistent run time. This algorithm utilizes the concept of merging two sorted halves of an array together by comparing each element in the two halves and arranging them from smallest to largest. In order to get the two sorted halves, merge sort is run recursively on each individual half until a subsection of the array can no longer be split in half again.
From experience, I know that merge sort can initially be very difficult to understand due to the recursive complexity in this algorithm. However, I was able to grasp this concept by walking through an example and visually seeing what is happen at each individual step. We will walk through a simple example together before moving to the code implementation.
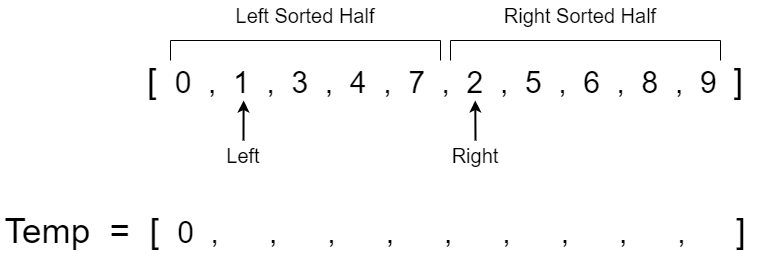
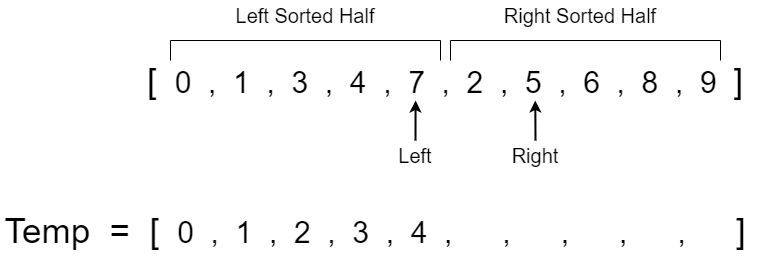
To begin our example, let's suppose we have two sorted halves of an array that we want to merge together. In order to merge these halves together and sort them in ascending order we need to compare the smallest value in the left sorted half with the smallest value in the right sorted half. We can achieve this by placing a left pointer at the smallest index location of the left sorted half and a right pointer at the smallest index location of the right sorted half.
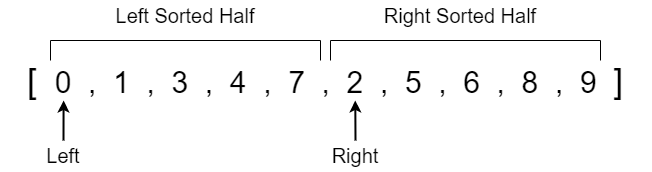
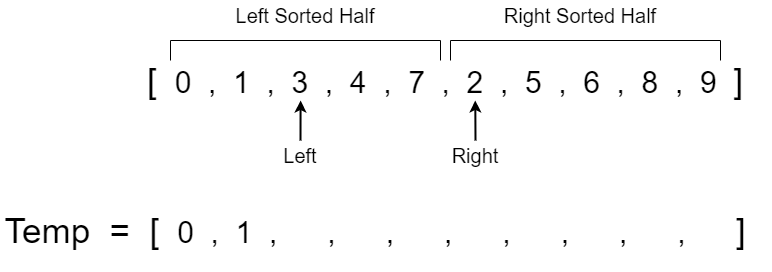
We can now ask whether the value at the left pointer or right pointer is smaller. Visually we can see that the left pointer has a value of 0 while the right pointer has a value of 2. 0 is smaller than 2 so we know that 0 must be placed at the first index of our array. To make merge sort simpler we will create a temporary array to hold the sorted values then overwrite the original array after we have all the elements in sorted order. After we copy a value to the temp array, we move the pointer at that value to the next item in the respective half. Since we copied over the value 0, we move the left pointer to the next index which has a value of 1.
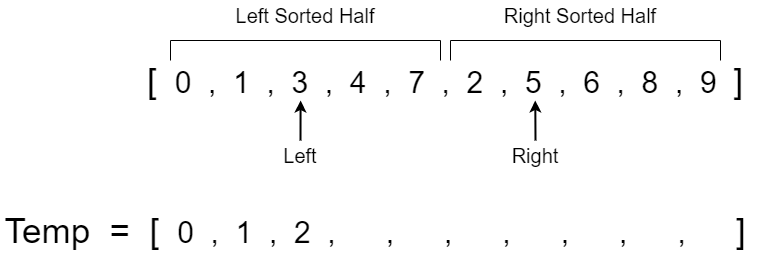
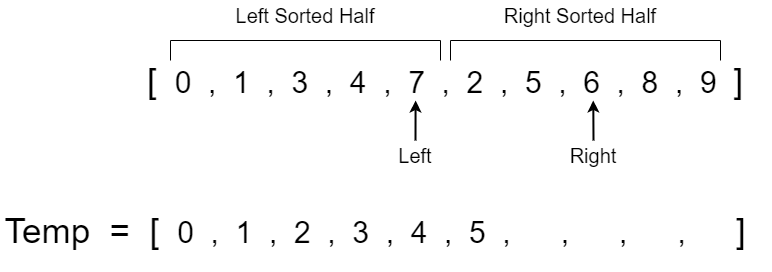
We now repeat the comparison of the left and right pointers and continue to take the smaller value. The left pointer has a value of 1 while the right pointer has a value of 2 so we copy the value 1 to the next available spot in the temp array and increment the left pointer.
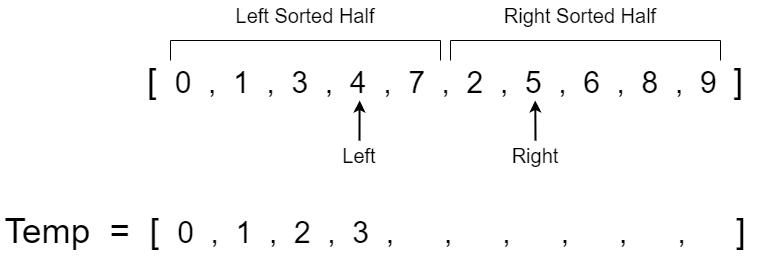
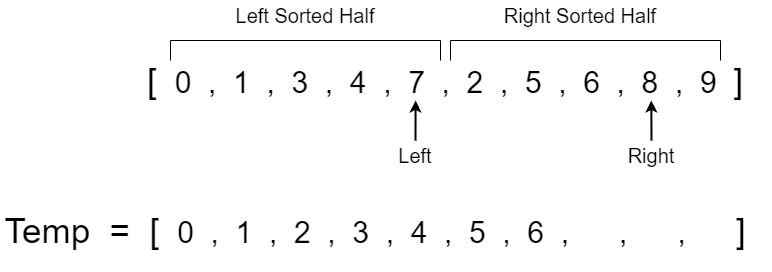
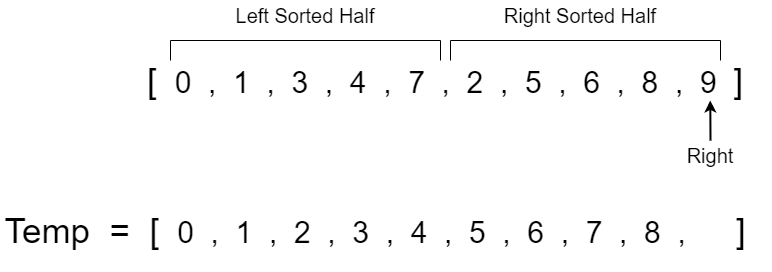
The left pointer now has a value of 3 and the right pointer has a value of 2. 2 is less than 3 so we copy 2 over to the temp array and increment the right pointer.
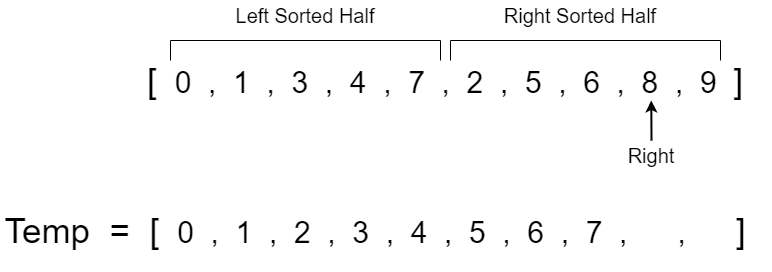
We will continue to repeat this step until we have compared all the values in both halves and have a completely sorted temp array. Note that once the left or right pointer reaches the end of their respective half we just copy over the remaining values from the pointer that hasn't reached the end yet.
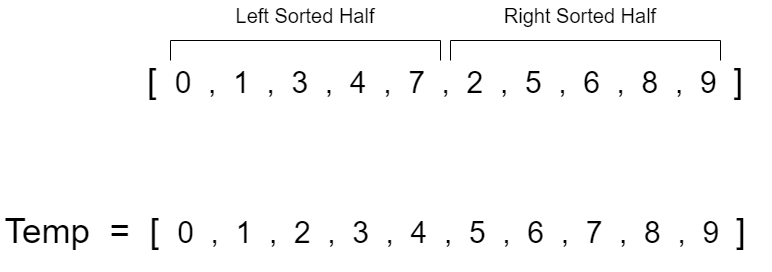
The left pointer has now reached the end of it's respective half so now we just have to copy the remaining values from the right half section of the array.
Once we have completely filled the temp array with the values from the original array in sorted order, all we have to do now is remember to overwrite the values from the temp array over to our original array.
The big question now is how do we get our array into two sorted halves? This is where recursion comes into play as we have to divide each respective half into another half until we reach a base condition. The base condition may not be obvious at first, but if we think about splitting an array into halves multiple times we will eventually reach a point where we have a single element that we can no longer split into two separate halves. Thinking about this in more detail, if we have a single element representing a single half then that half is already sorted since there is only one element. Let's walk through this recursive process to better understand how this is working.
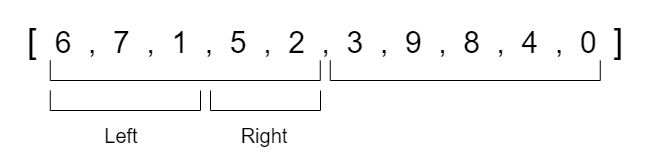
Given this unsorted array of numbers let's divide it into two separate halves.
We will now look at the left half and divide that section of the array into two separate halves.
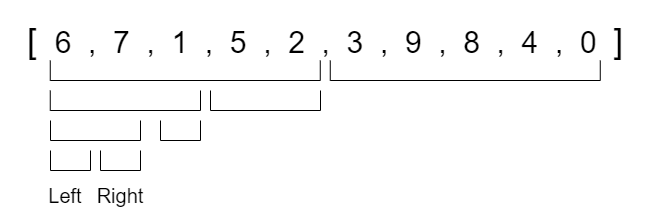
We will continue to look at the new left half and split that into half again.
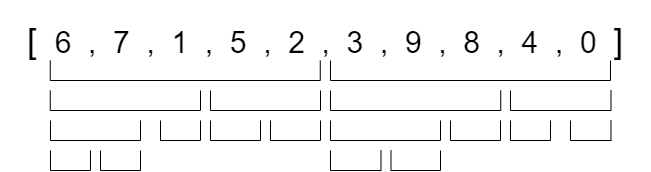
We continue to divide the left halves into two until we reach our base condition which is when we are no longer able to split the section into half again.
Here we can see that we reached a point where we can no longer split the sections into halves. This is our base condition since we can see that the left section contains a single element 6 which is sorted since it is the only element in its section and the right section contains the single element 7 which is also sorted since it is the only element. We now combine the two sorted halves to get a sorted subsection and work our way up the recursive stack until the entire array is sorted. The follow image shows the recursive stack that would occur on the entire array.
Once we have a good understanding of how merge sort works, the implementation of the code is quite simple. The first step is to create a function that accepts an integer array to be sorted as the parameter. This function doesn't need to return a value since arrays are pass by reference in Java which means that the array will retain any modifications that we make on it.
public static void
mergeSort(
int
[] nums){
}
Inside of this function we want to create a temporary array with the same size as our original array which will help us during the comparison process of the two sorted halves.
public static void
mergeSort(
int
[] nums){
int
[] temp =
new int
[nums.length];
}
We now want to make a call to our recursive function. This recursive function will take in the array to be sorted, the temp array, the left most index of the array, and the right most index of the array as parameters.
public static void
mergeSort(
int
[] nums){
int
[] temp =
new
int[nums.length];
mergeSortRecursive(nums, temp, 0, nums.length-1);
}
public static void
mergeSortRecursive(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
}
Inside of our recursive merge sort function we can start off by defining the base case condition that would terminate the recursive call. We have already discussed this during our example walk through and have concluded that we want to exit the recursive call when we have a single element that can no longer be divided into two. In other terms, this will happen when our leftStart pointer is equal to the rightEnd pointer. So we can say that we want to return out of the function if the leftStart pointer is greater than or equal to the rightEnd pointer.
public static void
mergeSort(
int
[] nums){
int
[] temp =
new int
[nums.length];
mergeSortRecursive(nums, temp, 0, nums.length-1);
}
public static void
mergeSortRecursive(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
}
If we haven't reached our base case yet then we need to divide our current section into two halves. To do this we need to find the middle element in the subsection which can be done by finding the middle index value between leftStart and rightEnd.
public static void
mergeSort(
int
[] nums){
int
[] temp =
new int
[nums.length];
mergeSortRecursive(nums, temp, 0, nums.length-1);
}
public static void
mergeSortRecursive(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
mid = leftStart + (rightEnd - leftStart)/2;
}
Now we want to recursively call merge sort on each respective half. For the left side, this will be between leftStart and mid. While the right side will be between mid + 1 and rightEnd.
public static void
mergeSort(
int
[] nums){
int
[] temp =
new int
[nums.length];
mergeSortRecursive(nums, temp, 0, nums.length-1);
}
public static void
mergeSortRecursive(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
mid = leftStart + (rightEnd - leftStart)/2;
mergeSortRecursive(nums, temp, leftStart, mid);
mergeSortRecursive(nums, temp, mid + 1, rightEnd);
}
Lastly, we need to merge the two sorted halves together which is the meat and potatoes of the algorithm. To do this we will create a new function called mergeHalves where we compare each value in the sorted halves and copy them to the temporary array prior to overwriting our original array.
public static void
mergeSort(
int
[] nums){
int
[] temp =
new int
[nums.length];
mergeSortRecursive(nums, temp, 0, nums.length-1);
}
public static void
mergeSortRecursive(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
mid = leftStart + (rightEnd - leftStart)/2;
mergeSortRecursive(nums, temp, leftStart, mid);
mergeSortRecursive(nums, temp, mid + 1, rightEnd);
mergeHalves(nums, temp, leftStart, rightEnd);
}
public static void
mergeHalves(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
}
The first thing we need to do inside of the mergeHalves function is to set up our start and end pointers. The left pointer refers to the start of the left sorted half while the right pointer refers to the start of the right sorted half. The end of the left half will be the mid value while the end of the right half will be at the value of rightEnd.
public static void
mergeSort(
int
[] nums){
int
[] temp =
new int
[nums.length];
mergeSortRecursive(nums, temp, 0, nums.length-1);
}
public static void
mergeSortRecursive(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
mid = leftStart + (rightEnd - leftStart)/2;
mergeSortRecursive(nums, temp, leftStart, mid);
mergeSortRecursive(nums, temp, mid + 1, rightEnd);
mergeHalves(nums, temp, leftStart, rightEnd);
}
public static void
mergeHalves(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
int
left = leftStart;
int
leftEnd = leftStart + (rightEnd - leftStart)/2;
int
right = leftEnd + 1;
}
We will also need an additional variable called 'index' to tell us what the next avaiable spot in the temp array will be. Note that index is initialized to leftStart and not 0 because we could potentially be merging a subsection starting somewhere in the middle of the array.
public static void
mergeSort(
int
[] nums){
int
[] temp =
new int
[nums.length];
mergeSortRecursive(nums, temp, 0, nums.length-1);
}
public static void
mergeSortRecursive(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
mid = leftStart + (rightEnd - leftStart)/2;
mergeSortRecursive(nums, temp, leftStart, mid);
mergeSortRecursive(nums, temp, mid + 1, rightEnd);
mergeHalves(nums, temp, leftStart, rightEnd);
}
public static void
mergeHalves(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
int
left = leftStart;
int
leftEnd = leftStart + (rightEnd - leftStart)/2;
int
right = leftEnd + 1;
int
index = leftStart;
}
We can now walk through each of the halves to retrieve the smallest value and populate the temp array. Note that we will terminate when either the left pointer or right pointer reaches the end of their half. If we copy over the value at the left pointer, we will increment the left pointer. If we copy over the value at the right pointer, we will increment the right pointer. We then increment the index pointer after we copy over a value to move on to the next available spot in the temp array.
public static void
mergeSort(
int
[] nums){
int
[] temp =
new int
[nums.length];
mergeSortRecursive(nums, temp, 0, nums.length-1);
}
public static void
mergeSortRecursive(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
mid = leftStart + (rightEnd - leftStart)/2;
mergeSortRecursive(nums, temp, leftStart, mid);
mergeSortRecursive(nums, temp, mid + 1, rightEnd);
mergeHalves(nums, temp, leftStart, rightEnd);
}
public static void
mergeHalves(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
int
left = leftStart;
int
leftEnd = leftStart + (rightEnd - leftStart)/2;
int
right = leftEnd + 1;
int
index = leftStart;
while
(left <= leftEnd && right <= rightEnd){
if
(nums[left] <= nums[right]){
temp[index] = nums[left];
left++;
}
else if
(nums[left] > nums[right]){
temp[index] = nums[right];
right++;
}
index++;
}
}
Once we exit this initial while loop condition, we still have to copy over the remaining elements from the half of whichever pointer that did not reach the end. To do this, we can create two while loop conditions similar to the first while loop but specifically targets the left and right array halves. Note that one of these loops will not run since we are just copying over the values from the half whose pointer did not reach the end.
public static void
mergeSort(
int
[] nums){
int
[] temp =
new int
[nums.length];
mergeSortRecursive(nums, temp, 0, nums.length-1);
}
public static void
mergeSortRecursive(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
mid = leftStart + (rightEnd - leftStart)/2;
mergeSortRecursive(nums, temp, leftStart, mid);
mergeSortRecursive(nums, temp, mid + 1, rightEnd);
mergeHalves(nums, temp, leftStart, rightEnd);
}
public static void
mergeHalves(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
int
left = leftStart;
int
leftEnd = leftStart + (rightEnd - leftStart)/2;
int
right = leftEnd + 1;
int
index = leftStart;
while
(left <= leftEnd && right <= rightEnd){
if
(nums[left] <= nums[right]){
temp[index] = nums[left];
left++;
}
else if
(nums[left] > nums[right]){
temp[index] = nums[right];
right++;
}
index++;
}
while
(left <= leftEnd){
temp[index] = nums[left];
left++;
index++;
}
while
(right <= rightEnd){
temp[index] = nums[right];
right++;
index++;
}
}
Lastly, we just iterate through the temp array from leftStart to rightEnd and overwrite the original array's values with the temp array values.
public static void
mergeSort(
int
[] nums){
int
[] temp =
new int
[nums.length];
mergeSortRecursive(nums, temp, 0, nums.length-1);
}
public static void
mergeSortRecursive(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
if
(leftStart >= rightEnd){
return
;
}
int
mid = leftStart + (rightEnd - leftStart)/2;
mergeSortRecursive(nums, temp, leftStart, mid);
mergeSortRecursive(nums, temp, mid + 1, rightEnd);
mergeHalves(nums, temp, leftStart, rightEnd);
}
public static void
mergeHalves(
int
[] nums,
int
[] temp,
int
leftStart,
int
rightEnd){
int
left = leftStart;
int
leftEnd = leftStart + (rightEnd - leftStart)/2;
int
right = leftEnd + 1;
int
index = leftStart;
while
(left <= leftEnd && right <= rightEnd){
if
(nums[left] <= nums[right]){
temp[index] = nums[left];
left++;
}
else if
(nums[left] > nums[right]){
temp[index] = nums[right];
right++;
}
index++;
}
while
(left <= leftEnd){
temp[index] = nums[left];
left++;
index++;
}
while
(right <= rightEnd){
temp[index] = nums[right];
right++;
index++;
}
while
(left <= leftEnd){
temp[index] = nums[left];
left++;
index++;
}
for
(
int
i=leftStart; i<=rightEnd; i++){
nums[i] = temp[i];
}
}
We have now completed the merge sort algorithm. Give this algorithm a try on an unsorted integer array and verify that the array becomes sorted!