Depth First Search (DFS) is an algorithm used to traverse a graph by first exploring deep before exploring wide. This algorithm ensures that every path starting from a particular node has been accounted for. We will walk through a simple example to explore and understand the concept of DFS.
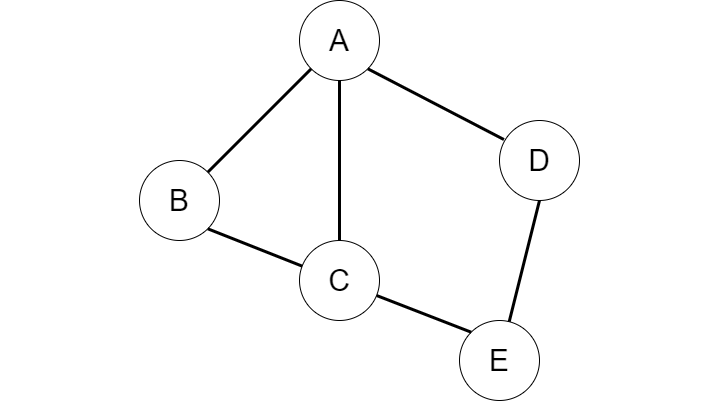
Let’s suppose we have a graph that contains 5 nodes with the letters A, B, C, D, and E and we want to determine whether a path exists between nodes A to E.
Visually, we can see that there are multiple paths that could lead us from node A to E. Three trivial paths that we can immediately see are [A->B->C->E], [A->C->E], and [A->D->E]. Another more complicated path could be [A->B->C->A->D->A->B->C->E], which is valid however we are visiting the same nodes multiple times before reaching the desired destination node. In order to avoid the repetition of already visited paths we will have a data structure that keeps track of the nodes that we have already visited so that we avoid any possible cycles.
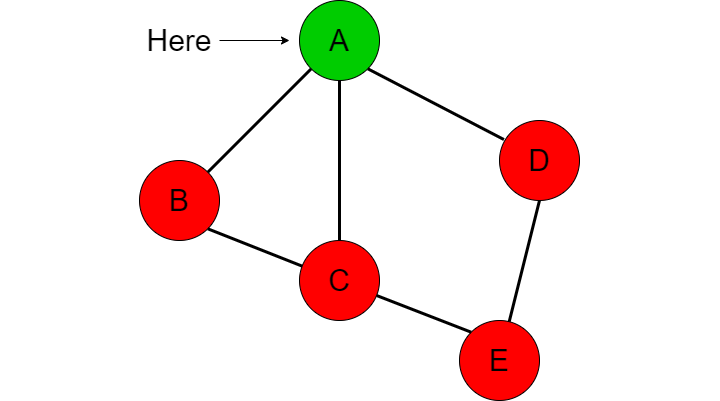
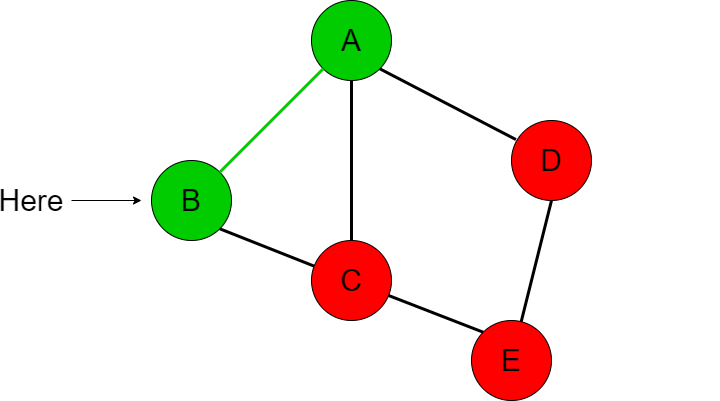
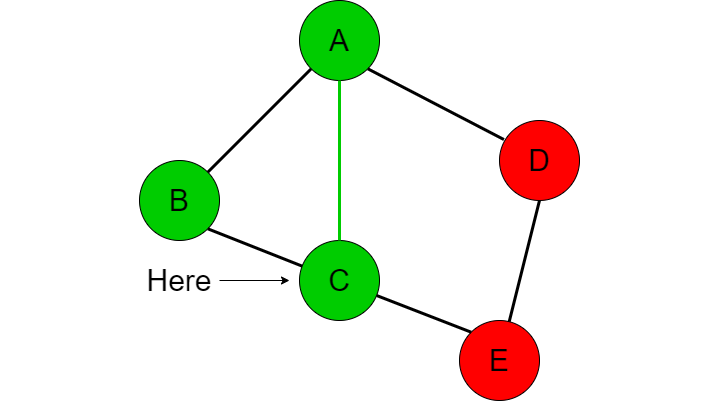
In the following example, nodes that are represented in red have not been visited while nodes in green are nodes that have been visited before.
The depth first search approach will first start at node A and compare whether A is equal to the destination node that we are searching for, in this case E.
Since A is not equal to E, we need to see what options/paths we have access to. These paths are the adjacent nodes that A is connected to which are B, C and D. If we recall the Graph data structure, we know that every node has a LinkedList which contains the adjacent nodes that the current node is connected to, we will call this list ‘adjacent’. For our example, we can assume that node A’s adjacent list looks like this [B, C, D]. Since B is the first item in the list we will choose to take that path before checking paths C and D.
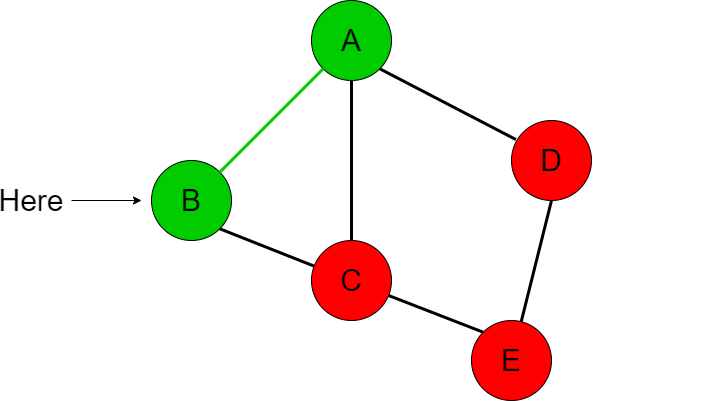
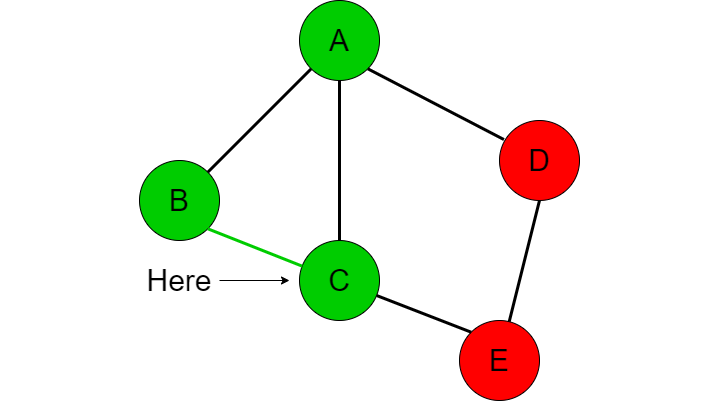
We are now at node B so we compare if B is equal to our destination node E. This is not the case, so we now check what paths we can take from node B. Node B has an adjacent list that contains [A, C] in this order. Thus we first go to node A before going to C.
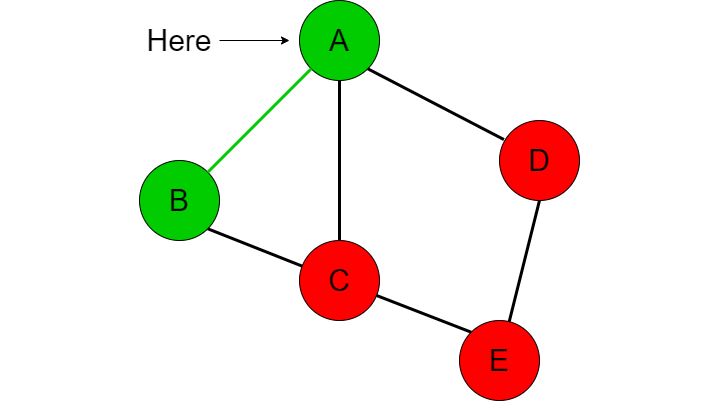
Now we have already been to node A and checked if A is equal to E so this is redundant. This is where we need another data structure to contain all of the nodes we have already visited. So far we have travelled to node A and node B so this ‘visited’ list will contain those two nodes. If we have visited a node already then we want to just go back to the previous node and check the next item in the adjacent node list. In this case, we’ve been to A so we return back to B and check the next item in node B’s adjacent list which is C.
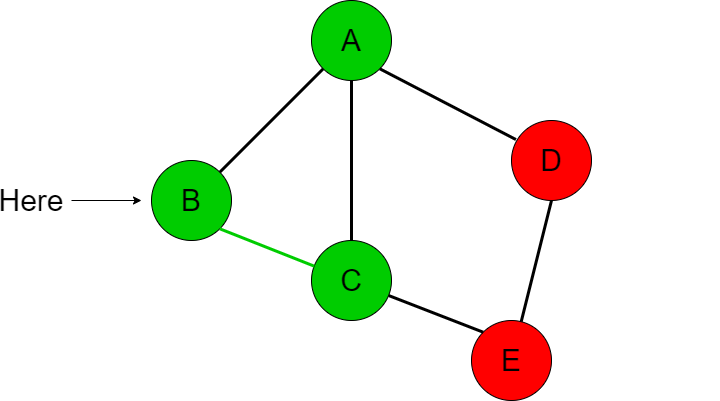
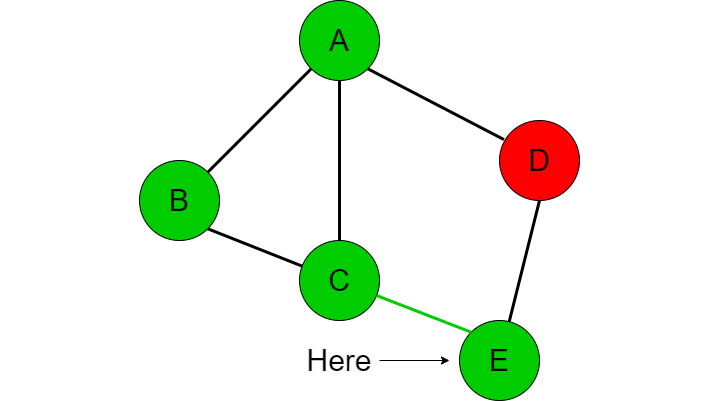
We now check if we have visited C (which we have not), add it to the visited list, then compare whether C is the destination node we are looking for. We repeat this procedure again with the adjacent nodes of C which looks like this [B, A, E]. We first go to B but realize we have already been there before so we go back to C.
Now we go to A, but similarly we have already been there before too so we go back to C.
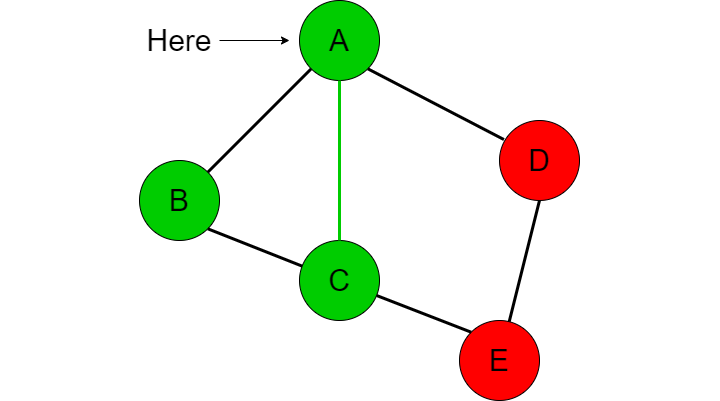
We now go to E where we realize that this is the destination node that we are looking for and will return true since we have confirmed that there is a path from A to E.
Note that we did not end up checking the adjacent nodes from A to C or A to D because we went down the B path which lead us down the path to C then down the path to E. This is the concept of exploring deep before wide. If we were to explore wide, we would check all of the adjacent nodes connected to A (B, C, D) prior to checking the connections of B, C, and D. Exploring wide before deep is an example of the breadth first search (BFS) algorithm and is another topic that I cover under my algorithms section.
Also note that we did not end up visiting node D in our example, however if we were to run the DFS algorithm searching for a specific node that doesn't exist in the graph then we would end up visiting all of the nodes. DFS can be implemented in a variety of ways depending on the problem you are trying to solve, however the key concept of searching deep before wide is what your DFS algorithm should be built around.
The DFS algorithm can be implemented both iteratively and recursively. The following code implementation will be done recursively, however it can be slightly modified to convert it into an iterative solution.
To begin the implementation of DFS, we will create a function called hasPathDFS() which accepts two parameters. The first parameter is the value of the start location and the second is the value of the destination that we are searching for. We will assume that our graph will contain strings as values. This function will return true if it can find a valid path from the start node to the destination node or else it will return false.
public boolean
hasPathDFS(String start, String destination){
}
The first task to implement is to get the node references that relate to the input parameters. We can find the node references because we know that the Graph data structure contains a HashMap (which we will refer to as 'nodeLookup') containing all of the node objects in the graph.
public boolean
hasPathDFS(String start, String destination){
Node s = nodeLookup.get(start);
Node d = nodeLookup.get(destination);
}
Before we begin traversing for the node, we can perform a quick check to make sure that the nodes exist in the graph. If either of the nodes do not exist in the graph then there is no reason to go searching for whether there is a path between them.
public boolean
hasPathDFS(String start, String destination){
Node s = nodeLookup.get(start);
Node d = nodeLookup.get(destination);
if
(s ==
null
|| d ==
null
){
return false
;
}
}
The next item to consider in the function is how to keep track of the nodes that we have already visited. This can easily be done using a Set data structure where we continue to update the nodes in this set every time we visit a new node.
public boolean
hasPathDFS(String start, String destination){
Node s = nodeLookup.get(start);
Node d = nodeLookup.get(destination);
if
(s ==
null
|| d ==
null
){
return false
;
}
HashSet<Node> visited =
new
HashSet<Node>();
}
We have now prepared the basic items for our DFS algorithm, however we now need to make a call to another function which will be the recursive function that performs the actual DFS. We will call this recursive function dfs(), which will search for the destination node and return true if it has found it.
public boolean
hasPathDFS(String start, String destination){
Node s = nodeLookup.get(start);
Node d = nodeLookup.get(destination);
if
(s ==
null
|| d ==
null
){
return false
;
}
HashSet<Node> visited =
new
HashSet<Node>();
return
dfs(s, d, visited);
}
We have completed the structure for the hasPathDFS() function and can now move on to implementing the dfs() recursive function that performs the actual search algorithm.
This function will return a boolean based on whether it has found the destination node or not. It will accept three parameters that correspond to the current node, destination node, and visited HashSet data structure.
public boolean
dfs(Node c, Node d, HashSet<Node> visited){
}
The first thing we need to check is to see if we have visited this current node that we are on before and if we have then we immediately return false. If we have not been to this node before then we want to add it to our visited set list.
public boolean
dfs(Node c, Node d, HashSet<Node> visited){
if
(visited.contains(c)){
return false
;
}
visited.add(c);
}
Next we want to check if the current node that we are on is the destination node that we are looking for. If it is then we can return true.
public boolean
dfs(Node c, Node d, HashSet<Node> visited){
if
(visited.contains(c)){
return false
;
}
visited.add(c);
if
(c.equals(d)){
return true
;
}
}
Now if the current node doesn't match the destination node, we must check the adjacent nodes of the current node. This can be implemented using a for each loop since we have access to the current node's adjacent LinkedList.
public boolean
dfs(Node c, Node d, HashSet<Node> visited){
if
(visited.contains(c)){
return false
;
}
visited.add(c);
if
(c.equals(d)){
return true
;
}
for
(Node adj: c.adjacent){
}
}
Inside of the for loop, we will make our recursive call to check if any adjacent nodes down the line are equal to the destination node. If one of the nodes down the line is equal to the destination node then we can return true up the stack.
public boolean
dfs(Node c, Node d, HashSet<Node> visited){
if
(visited.contains(c)){
return false
;
}
visited.add(c);
if
(c.equals(d)){
return true
;
}
for
(Node adj: c.adjacent){
if
(dfs(adj, d, visited)){
return true
;
}
}
}
Finally, if we have exhausted all of the adjacent nodes and haven't found a path to the destination then we return false.
public boolean
dfs(Node c, Node d, HashSet<Node> visited){
if
(visited.contains(c)){
return false
;
}
visited.add(c);
if
(c.equals(d)){
return true
;
}
for
(Node adj: c.adjacent){
if
(dfs(adj, d, visited)){
return true
;
}
}
return false
;
}
The depth first search algorithm can be represented by the completed hasPathDFS() and dfs() functions which are shown below.
public boolean
hasPathDFS(String start, String destination){
Node s = nodeLookup.get(start);
Node d = nodeLookup.get(destination);
if
(s ==
null
|| d ==
null
){
return false
;
}
HashSet<Node> visited =
new
HashSet<Node>();
return
dfs(s, d, visited);
}
public boolean
dfs(Node c, Node d, HashSet<Node> visited){
if
(visited.contains(c)){
return false
;
}
visited.add(c);
if
(c.equals(d)){
return true
;
}
for
(Node adj: c.adjacent){
if
(dfs(adj, d, visited)){
return true
;
}
}
return false
;
}