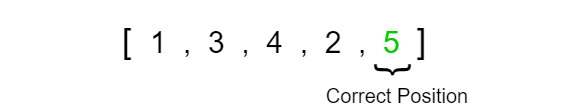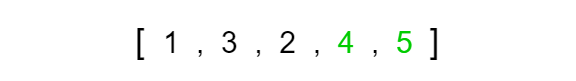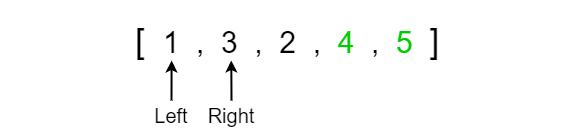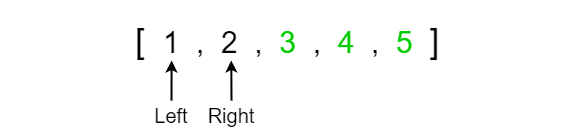The bubble sort algorithm is a beginner friendly sorting algorithm that is easy to understand and translate into code. Similar to any sorting algorithm, the purpose is to sort the values into a desired sequence usually in ascending order from left to right.
Bubble sort achieves this task by looking at the values in the first two index positions of an array and compares which value is larger. Since we are sorting from smallest to largest, we want the smaller values to be on the left side and the larger values to be on the right side. If the value located at the left index position is smaller than the value at the right index position then we know that the values in the current pairing are in the correct order and can move onto the next index pairing. Otherwise, if the value at the left index position is greater than the value at the right index position then we must swap the placement of the values before moving onto the next index pairing. The next pairing will always be the indexes of the previous pairing plus 1, thus one of the values in the old pair will be evaluated in the new pair. This comparison between pairs is repeated until the end of the array has been reached where the largest value will eventually “bubble” to the end of the array. This entire procedure is repeated until all the values in the array are in their correct positions, resulting in a sorted array.
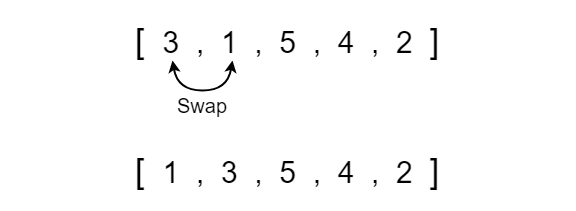
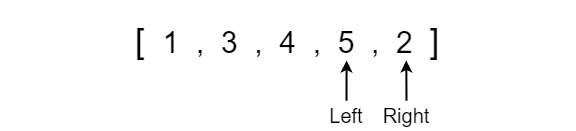
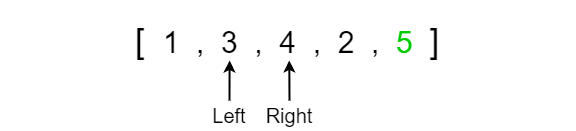
To better conceptualize this algorithm we will walk through a simple example. In the following example, we start off by comparing the first two elements in the array. The reference pointer “Left” is initially set to index 0 of the array while the pointer “Right” is set to index 1. We compare whether the left value is greater than the right value and if so then we swap the positions of the values with one another since we want the smaller value on the left side and the larger value on the right.
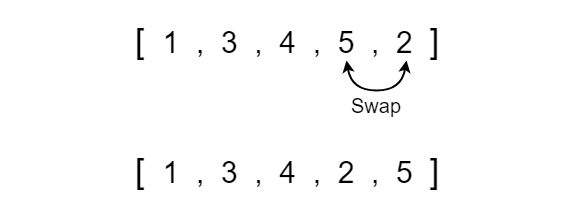
In this case, the value at the left index is 3 and the value at the right index is 1. Since the value at the left index is greater than the value at the right index we must swap the values.
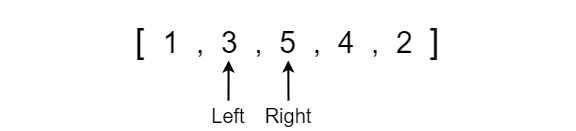
After comparing the first pair, we move the left and right pointers up one position to index 1 and index 2 respectively.
We now compare the values at the indexes where we see that 3 is smaller than 5 so we can move onto the next pairing since these values are in the correct position.
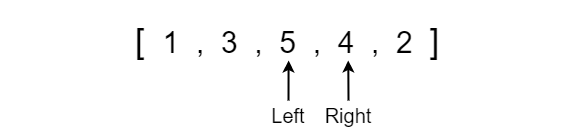
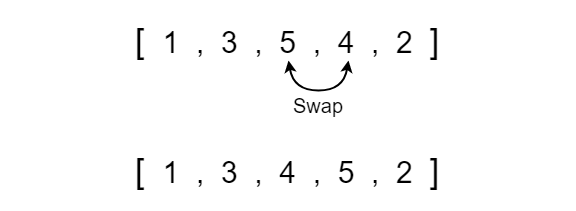
Again we move the left and right indexes up a position to index 2 and index 3 then compare the values. Since 5 is greater than 4 we know that it should be on the right side and 4 should be on the left side so we must swap the two values.
We now compare the last index pairing and have to swap the values since 5 is greater than 2. We know that this is the last pairing since the right pointer has reached the end of the array and has no other values to evaluate.
We have now reached the end of our array and the result is that 5 has landed in its correct position since it is the largest value in the array and thus must be at the very end of the array. We can now repeat the same steps until each of the next largest values continue to bubble to the right side of the array. This will eventually result in our array being completely sorted.
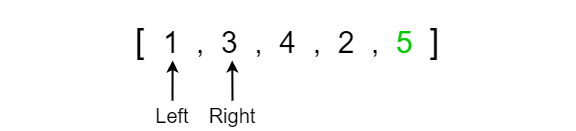
Note that for the last comparison, when we determined the correct value at index 1 it automatically determines the placement for the value at index 0 as well. Knowing this, we can save ourselves an additional iteration when we translate this algorithm into code.
The bubble sort algorithm is pretty easy to implement since we are just iterating through the array and swapping the values of pairs if the left value is greater than the right value. The key to this algorithm is knowing how many times we need to iterate through the array.
If we think about the loop structure, we know that we need a for loop that iterates through the entire array and bubbles the largest value to the end of the array (this will be the inner loop). Now, how many times will we need to repeat the bubbling of the next largest value to its correct position? The answer is simple, we will have to repeat this N times where N is the number of elements in the array since all of the values need to bubble to their correct position. The reason for this is that each time we run through the inner loop we are only placing one of the values in the correct position. Since we want all of the values to be in the correct position we will need an outer loop that runs N number of times. We can slightly optimize this since we know that running the Nth iteration and Nth - 1 iteration will result in the same operation so really we only need to run the outer loop N - 1 times. If this slight optimization is confusing you can just set the outer loop to run N number of times as this will still result in the correct solution.
To begin constructing this algorithm, we will start by creating a function called 'bubbleSort' which will accept an array of integers as a parameter. Since we are manipulating the values in the array within the function, and arrays are pass by reference in Java, we do not have to return anything back to the main function and can set the return type to void. Pass by reference simply means that an object being changed within a function will retain the changes made to it.
public static void
bubbleSort(
int
[] nums){
}
We will now add the outer for loop which will start at 0 and iterate N - 1 number of times. Recall that N is the number of elements in the array which can be access via the length attribute. Note that this for loop corresponds to the number of values that need to bubble to their correct placement in the array.
public static void
bubbleSort(
int
[] nums){
for
(
int
i=0; i<nums.length-1; i++){
}
}
We will now add the inner loop which will iterate through the array and compare the values at the left and right indexes. Since we are walking through each PAIR in the array this will need to be done N - 1 number of times. To simplify this, we will start the loop counter at a value of 1 and iterate until hitting the last index in the array. An easy way to understand why we run N - 1 number of times is because the right pointer will start at index 1 and run until the last index in the array which equates to N - 1.
public static void
bubbleSort(
int
[] nums){
for
(
int
i=0; i<nums.length-1; i++){
for
(
int
j=1; j<nums.length; j++){
}
}
}
Now comes the interesting part of the algorithm. We need to compare each of the pairs and check whether the value at the left index is smaller or greater than the value at the right index, then swap the values if needed. We know that we want our left pointer to start at index 0 and our right pointer to start at index 1. We can utilize j to accomplish this by subtracting 1 from it to get the left pointer index and having j be the value of the right pointer index. As j increases so will the left and right index values.
Once we have established the left and right pointers, we now need to compare the values at these pointers. This comparison can be done with a simple if statement where we want to swap the values if the value at the left index is greater than the value at the right index. Swapping the pairs is now a simple operation where we utilize a tempNum variable to perform the swap.
public static void
bubbleSort(
int
[] nums){
for
(
int
i=0; i<nums.length-1; i++){
for
(
int
j=1; j<nums.length; j++){
if
(nums[j-1] > nums[j]){
int
tempNum = nums[j-1];
nums[j-1] = nums[j]
nums[j] = tempNum;
}
}
}
}
Our bubble sort function is now complete, however we can slightly optimize this function since we know that each time the inner for loop completes a full iteration of the array, the right most unsorted index position will become sorted. As such, we no longer need to compare that value in the next iteration and thus can update the inner for loop to iterate until nums.length - i.
public static void
bubbleSort(
int
[] nums){
for
(
int
i=0; i<nums.length-1; i++){
for
(
int
j=1; j<nums.length-i; j++){
if
(nums[j-1] > nums[j]){
int
tempNum = nums[j-1];
nums[j-1] = nums[j]
nums[j] = tempNum;
}
}
}
}
It is always good practice to consider the time complexity of an algorithm because we want to accomplish our desired task as efficiently as possible. It is also very important to know the time complexity of an algorithm so that we can compare it to other algorithms that perform the same task to evaluate which method is better. As we have discovered, bubble sort is a very straight forward algorithm to understand and implement. The time complexity of this algorithm however is pretty inefficient due to the fact that we are iterating through the array multiple times. We iterate through the array to bubble the largest value to the right side and repeat this operation for the number of elements in the array. This nested looping results in a quadratic O(N^2) time complexity which can be improved upon. As we explore other sorting algorithms, we will find that O(N^2) time is pretty slow since there are other sorting algorithms that can run in O(N*log N) time complexity such as merge sort and quick sort. It is good to keep in mind that even though there are faster sorting algorithms out there it does not mean that those algorithms are necessarily better since they may come with tradeoffs such as additional space usage. Bubble sort has a slow time complexity, however it has a great space complexity of O(1) since it doesn't require additional space due to the fact that all the sorting is done in place. If you are curious about other sorting algorithms, check out my sections on merge sort and quick sort!