Searching for a piece of data within a list is a very common operation that exists in many software applications. Some of the apps that we use on a daily basis utilize searching algorithms to make their apps user friendly and efficient. Take an app like Spotify for example, they have a huge database of songs in their collection and without their search feature you could be spending hours trying to find a particular song. Another example of where a searching algorithm is heavily used is in a dictionary. When we flip through a dictionary to find the definition of a specific word we are performing a searching algorithm. Both of these examples requires some sort of searching algorithm in order to accomplish the task of locating a piece of data.
If we expand on the Spotify example, one method of finding a song is to scroll through the entire library in alphabetical order until we have found the song we are looking for. This is a linear traversal algorithm that we are performing since we are scrolling through each of the songs from A to Z. This search method would be acceptable if we had a personal playlist of 10 songs that we were searching through. However, if Spotify was trying to find a song through its entire database it would not be very efficient to walk through the entire alphabet of songs from A to Z, especially if the song name started with a Z.
If we consider our dictionary example where we want to search for the word 'apple', intuitively we would open up our dictionary to the first page and search for the word 'apple' page by page. We would do this because we know that 'apple' starts with the letter A and is located somewhere near the beginning of the dictionary. This is very similar to the linear algorithm we discussed in the Spotify example as we are walking through each word in the dictionary until we find the word we are looking for. Now what if we wanted to search for the word 'rainbow'? Starting at the beginning of the dictionary and flipping through each page until finding the word 'rainbow' would not only be extremely slow, but tedious as well. Intuitively, we would flip to somewhere in the middle of the dictionary until we found words that start with letters close to R. We would continue to flip through chunks of pages until we narrow in on words that start with R, then we would repeat this process with the proceeding letters in the word 'rainbow' until we have found the word we are searching for. This operation we just perfomed is a form of binary search and we can immediately see how much more efficient this operation is compared to linearly searching through the entire dictionary.

There are a few points to discuss before moving onto the code implementation of binary search. Firstly, in order for binary search to work the list containing the data must be sorted in ascending order. This is one of the prerequisites that many people forget but it should be the first thing that comes to mind when considering using binary search. Secondly, in binary search we look for the middle element in the sorted array and compare it to the value we are searching for. In order to get the middle element in the array we need two pointers, left and right, which start at opposite ends of the array and move according to whether the middle element is greater than or less than the search value.
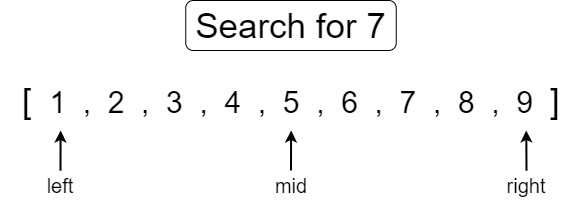
In the following example, the left pointer is located at index 0 and the right pointer is located at index 8. We get the middle index by finding the middle value between the left and right pointers which happens to be at index 4. We compare the middle value with our search value and compare whether it is equal, less than, or greater than the value we are searching for. Since the value at mid is 5 and the value we are searching for is 7, we can say that 7 must be located somewhere on the right side of the mid pointer. As such, we would then move our left pointer to the index position to the right of the mid pointer. We would not move the left pointer to the mid index position since we already know that it is not the value we are searching for and therefore can exclude it from the new search range.

Essentially, we have just eliminated half of the values in our array that we have to search through which are shown in red and are left with half of the values shown in green. We repeat this process again by finding the mid value in the new range and comparing it with our search value. In this scenario, we have 4 elements so there is no exact middle element but to simplify things we will always take the left middle element when dividing an even number of elements by 2.
We now compare the value at the mid pointer with the search value and we see that they are equal. In most cases, the function you write to implement binary search will require you to return the index of the value in the array which is equal to the mid pointer. If the target value does not exist in the array, then we would find that eventually the left pointer will be greater than the right pointer. Once this occurs we can be confident that the value does not exist in the array and can return a value of -1.
The basic structure of binary search is very simple to implement. The first step to implementing this algorithm is to make sure that the input array is sorted. Instead of implementing a sorting algorithm ourselves, I will be using a built in Java method that will perform the sorting so that we can focus primarily on implementing binary search. If you are interested in learning how to implement a sorting algorithm, check out my other pages on sorting algorithms.
public static int
binarySearch(
int
[] nums,
int
target){
Arrays.sort(nums);
}
Once we have the input array sorted we can now move onto implementing the binary search algorithm. To begin constructing this algorithm, we will need to initialize the left and right pointers that will give us the search range for the target value. Since we want to search the entire array we will set the left pointer to the first element in the array and the right pointer to the last element in the array.
public static int
binarySearch(
int
[] nums,
int
target){
Arrays.sort(nums);
int
left = 0;
int
right = nums.length-1;
}
The next step is to implement a while loop that will find the mid value between the left and right pointers, as well as compare the mid value to the target value that we are trying to find. If we go back to the example that we walked through, we can recall that we want to repeat this process as long as the left pointer is less than the right pointer or until we have found the target value. If we find the location of the target value during the loop, we will just return the index of that value which will exit out of the function. So this means that we want the while loop to run as long as the left pointer is less than or equal to the right pointer.
public static int
binarySearch(
int
[] nums,
int
target){
Arrays.sort(nums);
int
left = 0;
int
right = nums.length-1;
while
(left <= right){
}
}
Inside of the while loop we want to get the middle index from the left and right pointers. One way of performing this action is by adding the left and right values together then dividing the sum by 2. Because integers on a computer are limited to a specific size, we could possibly run into unexpected results if adding the left and right index values together exceeds the maximum integer value. To avoid this, we will subtract the right index with the left index then divide the calculation by 2 then add the left index to get the middle value. This is a better implementation to get the middle value between two points as it avoids causing unexpected results.
public static int
binarySearch(
int
[] nums,
int
target){
Arrays.sort(nums);
int
left = 0;
int
right = nums.length-1;
while
(left <= right){
int
mid = left + (right-left)/2;
}
}
We now want to write a conditional statement that will check whether the value at the mid index is equal to, less than, or greater than the target number. This can simply be done using an if else statement.
public static int
binarySearch(
int
[] nums,
int
target){
Arrays.sort(nums);
int
left = 0;
int
right = nums.length-1;
while
(left <= right){
int
mid = left + (right-left)/2;
if
(nums[mid] == target){
}
else if
(nums[mid] > target){
}
else if
(nums[mid] < target){
}
}
}
Inside of the conditional if statement we need to think about what operation we want to happen for each case. If the value at the mid index is equal to the target value then we can say that we found the value we are looking for and we will return the index position represented by the value of mid. If the target value is less than the mid value then we know that the value is potentially to the left of the mid pointer so we will have to update our right pointer to mid - 1. Similarly, if the target value is greater than the mid value then we know that it could potentially be on the right side of the mid pointer and thus we will update the left pointer to mid + 1. Note that we move the pointers to mid - 1 and mid + 1 because we have already checked if mid is equal to the value we are searching for so we can exclude it in the new search range.
public static int
binarySearch(
int
[] nums,
int
target){
Arrays.sort(nums);
int
left = 0;
int
right = nums.length-1;
while
(left <= right){
int
mid = left + (right-left)/2;
if
(nums[mid] == target){
return
mid;
}
else if
(nums[mid] > target){
right = mid - 1;
}
else if
(nums[mid] < target){
left = mid + 1;
}
}
}
The last thing we need to consider is if we are unable to find the value we are searching for in the array. This would cause us to exit the while loop and can just return a value of -1 to indicate that the target value could not be found.
public static int
binarySearch(
int
[] nums,
int
target){
Arrays.sort(nums);
int
left = 0;
int
right = nums.length-1;
while
(left <= right){
int
mid = left + (right-left)/2;
if
(nums[mid] == target){
return
mid;
}
else if
(nums[mid] > target){
right = mid - 1;
}
else if
(nums[mid] < target){
left = mid + 1;
}
}
return
-1;
}
We have now implemented a simple variation of the binary search algorithm where we look for a specific value in an array and return the index value if found. Binary search has multiple variations depending on what is being asked from the problem. Many variations of binary search will require either setting the left or right pointers to the mid position rather than mid + 1 and mid - 1 so it is always important to consider what you are trying to achieve by moving these pointers. Binary search may also require post processing similar to how we did some preprocessing by sorting the array before implementing binary search. Always consider what is being asked and how one might be able to slightly modify this structure to obtain the desired output.
One of the main reasons why we consider binary search as a go to search algorithm is due to its quick time complexity. Recall how we discussed finding a word in a dictionary by flipping through it in chunks rather than page by page. Binary search works the exact same way as we are removing chunks of data that we don't have to search through to optimize the amount of time that it takes to find what we are looking for. In more technical terms, we divide our data set in half every time until we approach the location of the target value. Mathematically, we know that given a set of data with N elements we can only divide the elements into two a specific number of times before we can no longer split the data set anymore. This is represented by the expression 2^x = N where x represents the amount of times we can divide N by 2. This expression can be rewritten as log(N) with a base of 2. Thus the time complexity of this algorithm is O(log(N)) which is vastly more efficient than the linear time complexity of O(N).





