Breadth First Search (BFS) is a searching algorithm that explores the nodes closest to the starting point before expanding outwards and exploring the rest of the nodes in the graph. BFS is often described as the search wide before deep algorithm because we stay as close to the starting point as possible before traversing deep into the graph. In order to stay close to the starting point, this algorithm requires a queue data structure to keep track of which node should be next in line to be searched. As the search expands outwards, the nodes connected to the current search node are added to the end of the queue until all the nodes in the graph have been visited.
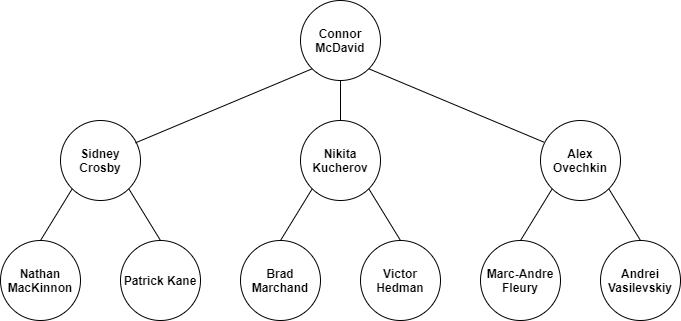
The best way to understand BFS is through a visual example which we will be applying on the following tree. We will be using a tree since it allows us to better visualize BFS than in a graph that contains cycles.
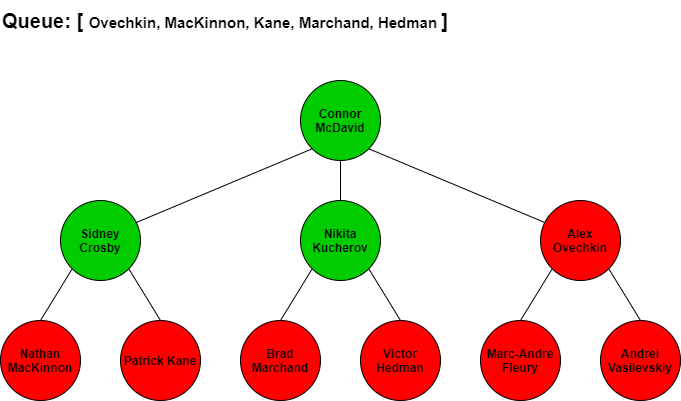
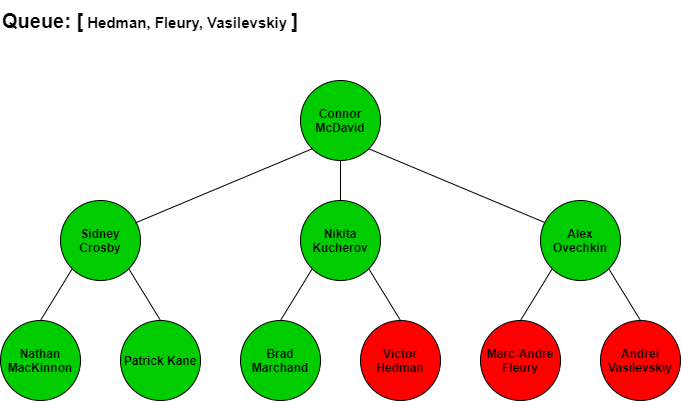
This tree contains the names of the top NHL players where each level represents the skill level of the player. We want to traverse the tree using the BFS algorithm, starting at the root (top player), to list out all the players in the order of their skill level.
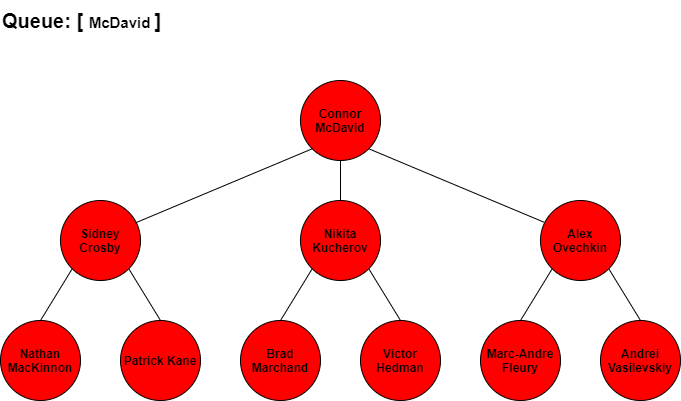
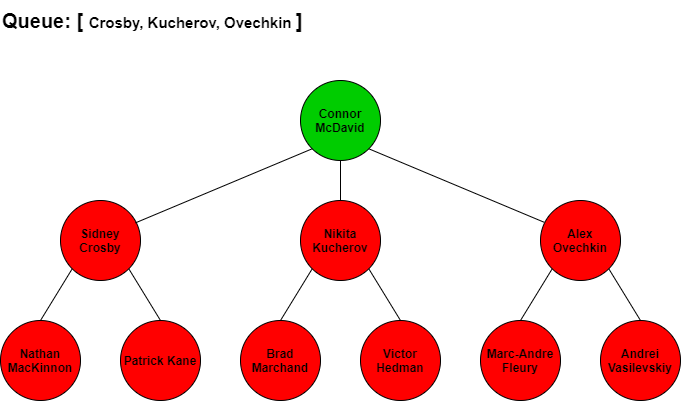
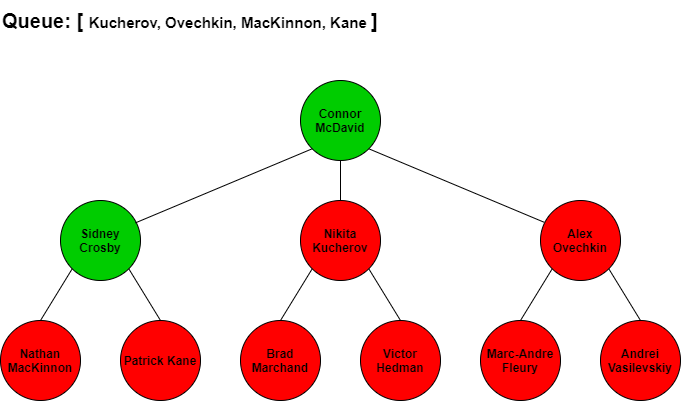
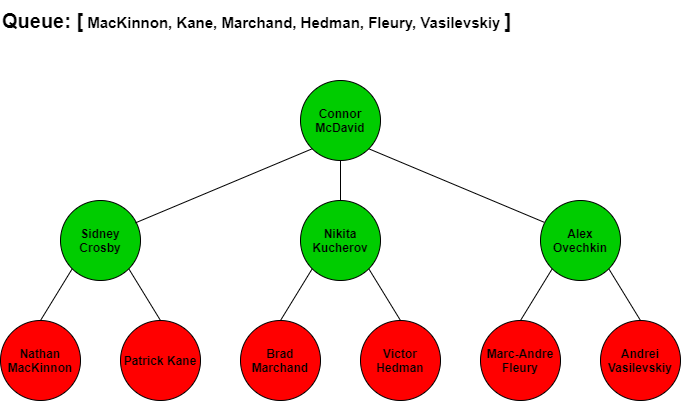
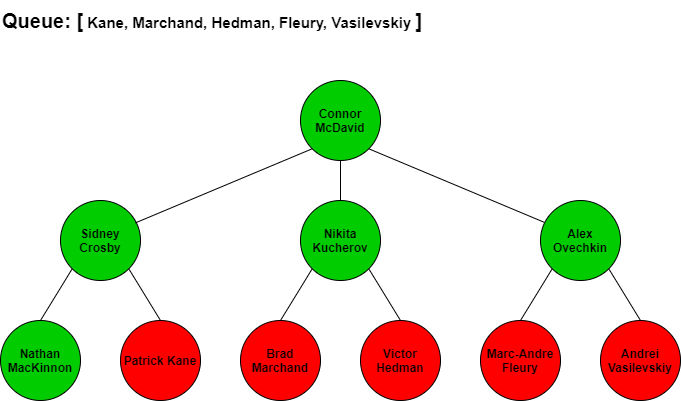
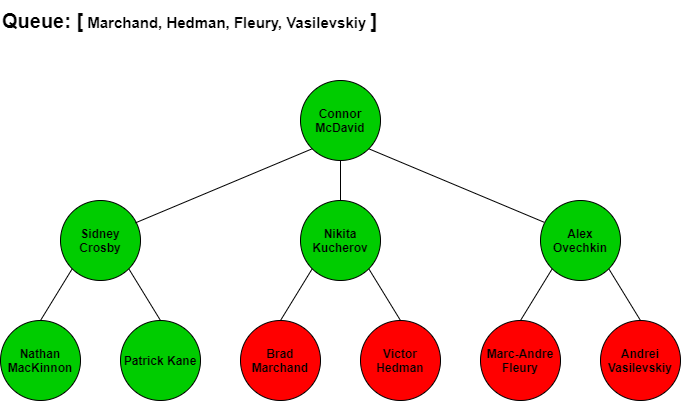
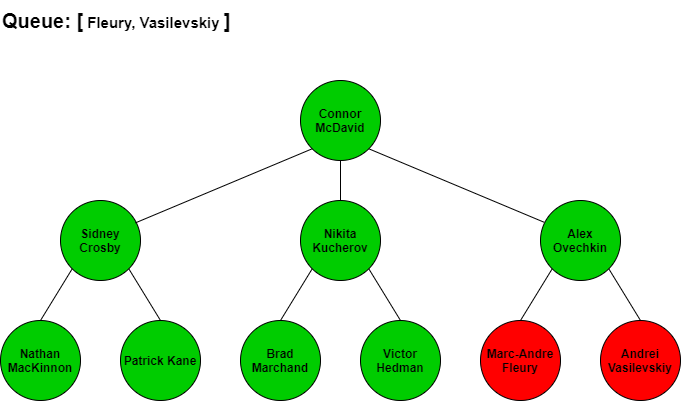
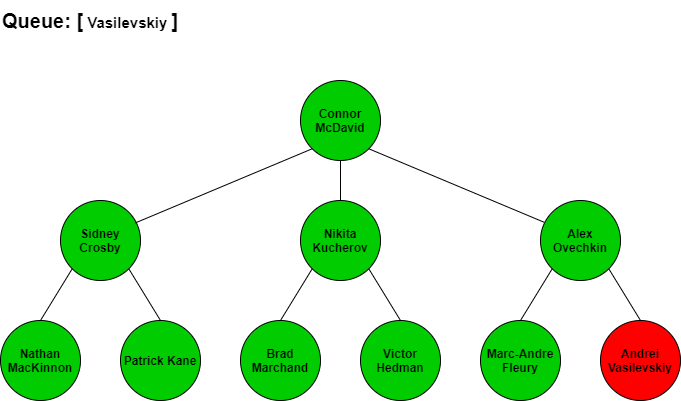
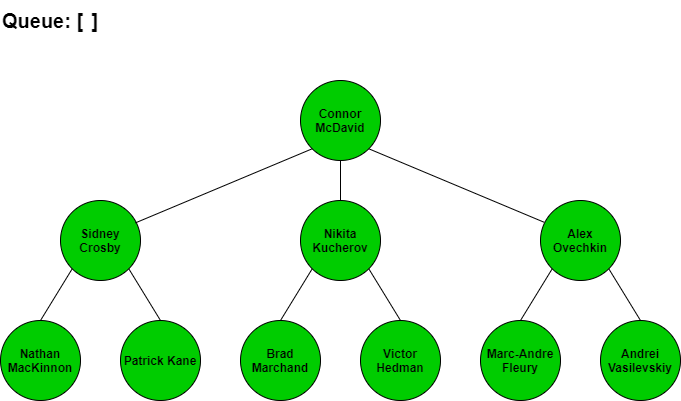
BFS would start at Connor McDavid then search for the next best players by seeing who Connor McDavid is linked to. From looking at the tree, McDavid is connected to Sidney Crosby, Nikita Kucherov, and Alex Ovechkin. We would add these three names in that order to our queue so we know who to check next. Since Crosby is next in our queue, we would traverse to him and add all the players connected to him to the end of the queue. Kucherov is next in the queue after Crosby so we would traverse to him and add all his connections to the end of the queue. We continue to repeat this process until we have added all of the players in the tree to the queue and have iterated through each of the players in the queue.
The output of this BFS traversal would look like this:
The visual step by step BFS traversal of this tree would look like the following with the queue items at each stage. Note that when we traverse to the next player in the front of the queue we remove them from the queue list.
Similar to DFS, the BFS algorithm can be implemented both iteratively and recursively. The following code implementation will be done iteratively, however it can be slightly modified to become recursive. Note that this algorithm will built off of the Graph data structure and a good understanding of the Graph data structure is required before proceeding.
To begin the implementation of BFS, we will create the function called traverseGraphBFS() with a single parameter called 'start'. The start parameter will be the value of the node that we want our traversal to begin at. The following functions are tailored towards applying BFS on a graph that contains integers as the node values. The data type can simply be changed to fit the structure of the graph you want to apply BFS on.
public void
traverseGraphBFS(
int
start){
}
The next step is to get the node reference from our nodeLookup HashMap and determine if this node exists in our graph. If the start node doesn't exist in the graph we can immediately exit the function. Note that the nodeLookup HashMap is part of the Graph data structure, if you are unfamiliar with this concept check out my page on how to construct the Graph data structure from scratch before continuing.
public void
traverseGraphBFS(
int
start){
Node startNode = nodeLookup.get(start);
if
(startNode ==
null
){
return
;
}
}
Similar to DFS, we will need a data structure to keep track of the nodes we have already visited. We can use a HashSet called 'visited' to keep track of these nodes. Another data structure that we will need is a queue, as we recall this queue will hold the order of the nodes that we traverse next. We can use a LinkedList to represent this queue.
public void
traverseGraphBFS(
int
start){
Node startNode = nodeLookup.get(start);
if
(startNode ==
null
){
return
;
}
HashSet<Node> visited =
new
HashSet<Node>();
LinkedList<Node> queue =
new
LinkedList<Node>();
}
Now that we have created the queue, we need to add the first item to the queue to begin the BFS traversal. This will be the startNode that we had initialized earlier.
public void
traverseGraphBFS(
int
start){
Node startNode = nodeLookup.get(start);
if
(startNode ==
null
){
return
;
}
HashSet<Node> visited =
new
HashSet<Node>();
LinkedList<Node> queue =
new
LinkedList<Node>();
queue.add(startNode);
}
We can now begin writing the actual BFS logic. Since this is an iterative solution, we need to consider what the terminating case should be. We know that when we traverse a node we take the next node out of the start of the queue that we want to visit next. Thus our algorithm needs to run as long as there is an item in the queue. Therefore we can create a while loop where we continue to loop until we have exhausted all the items in our queue.
public void
traverseGraphBFS(
int
start){
Node startNode = nodeLookup.get(start);
if
(startNode ==
null
){
return
;
}
HashSet<Node> visited =
new
HashSet<Node>();
LinkedList<Node> queue =
new
LinkedList<Node>();
queue.add(startNode);
while
(!queue.isEmpty()){
}
}
Now if the queue is not empty, we can pop the next item in the queue and check if we have visited this node before. If we have visited this node before, then we continue the loop and pop the next item from the list. We can determine if we have been to a node before by checking if it exists in the visited HashSet data structure. If we have not been to this node before, then we will add this node to the visited set and print the value of the node to the console.
public void
traverseGraphBFS(
int
start){
Node startNode = nodeLookup.get(start);
if
(startNode ==
null
){
return
;
}
HashSet<Node> visited =
new
HashSet<Node>();
LinkedList<Node> queue =
new
LinkedList<Node>();
queue.add(startNode);
while
(!queue.isEmpty()){
Node currentNode = queue.pop();
if
(visited.contains(currentNode)){
continue
;
}
visited.add(currentNode);
System.out.println(currentNode.data);
}
}
The last step is to add the child/adjacent nodes of the current node to the end of the queue. This can be perform with a for each loop on the current node's adjacent LinkedList. The adjacent list is part of the Graph data structure and contains all the node connections from a particular node.
public void
traverseGraphBFS(
int
start){
Node startNode = nodeLookup.get(start);
if
(startNode ==
null
){
return
;
}
HashSet<Node> visited =
new
HashSet<Node>();
LinkedList<Node> queue =
new
LinkedList<Node>();
queue.add(startNode);
while
(!queue.isEmpty()){
Node currentNode = queue.pop();
if
(visited.contains(currentNode)){
continue
;
}
visited.add(currentNode);
System.out.println(currentNode.data);
for
(Node adj : currentNode.adjacent){
queue.add(adj);
}
}
}
This is the completed BFS algorithm which traverses all of the nodes closes to the starting node before expanding outwards into the graph. The key concept to remember in BFS is that the traversal explores the nodes closes to the start position before expanding outwards.